Как регулярно пополнять контент-план с помощью матрицы контента

Квадрант D: не срочно, не важно

В это поле вносятся все малозначительные задачи

Да, они приносят пользу и удовольствие от результата! Но одновременно с тем отодвигают человека от выполнения важного дела. Задачи из рассматриваемого квадрата Эйзенхауэра практически никак не влияют на нашу жизнь

К ним относятся, например, следующие:

Пример: пролистывая ленту новостей, вы увидели интересный пост, который захотелось просмотреть. Данная задача требует срочности? Нет

Она является важной? Нет, выполнять ее необязательно.

Дела из квадрата D следует выполнять в последнюю очередь. Идеальный вариант построения матрицы времени Эйзенхауэра – тот, в котором в данном окне будут значиться 1 – 3 плановых мероприятия. Помните: отдыхать и переключаться должен каждый. Но лучше это сделать с помощью похода в спортзал, бассейн или прогулки по парку в вечернее время.

Этот и другие инструменты вы можете изучить на онлайн-курсах менеджмента, например:

• Факультет Проджект-менеджмента от GeekBrains
• Профессия Менеджер проектов от Skillbox>
• Продакт-маркетолог с нуля до PRO от Нетологии

Матрица в Ворде

Работая в текстовом редакторе Ворд с нестандартными видами математических уравнений и формул, зачастую невозможно найти решение для вставки какого-то элемента. Вот, например, сделать матрицу в Ворде можно, но и здесь есть ограничения. На первый взгляд, кажется, что функционал ограничен и многие не знают, каким образом делается матрица 5 на 5 или 4 на 4, ведь нет такой структуры в допустимых вариантах. Максимальное значение, которое можно вставить это 3 на 3 – ошибочное мнение, которому подверглись многие пользователи Ворда. Давайте рассмотрим способ решения данной проблемы, и отныне для вас не будет границ в текстовом редакторе.

Как работать с таблицей Эйзенхауэра?

Прежде всего, нужно усвоить ряд правил.

Список дел лучше составлять с вечера. При этом не нужно заполнять всю таблицу сразу. Рекомендуем вам оставить немного места для систематизации планов и/или их дополнения. Начинать распределять задачи лучше с переноса незавершенных. Далее следует вносить в матрицу Эйзенхауэра новые задачи.

Количество дел на квадрат не должно превышать 8

Так вы избавитесь от лишней нагрузки и сможете сосредоточиться на выполнении самого важного. Выполнили задачу? Выделите ее цветом

С одной стороны, это поможет вам осознать, что вы быстро продвигаетесь в реализации своих планов, с другой – определить то, что уже выполнено.

Личные и профессиональные задачи лучше разделять. Если в вашей жизни проводится четкое разграничение между работой и семьей (вы работаете с 8.00 до 17.00), создайте две отдельные матрицы. Если ее нет, делать это необязательно.

Чтобы определить важность того или иного дела, задайте себе вопрос «Возникнут ли у меня проблемы, если я отложу эту задачу?». Чтобы определить, срочно его нужно выполнить или не срочно, дайте ответ на вопрос: «Если я отложу эту задачу, она потеряет актуальность?»

Воспользуйтесь шаблоном
Итак, чтобы составить матрицу приоритетов Эйзенхауэра, необходимо взять белый лист бумаги

Приняв во внимание всю представленную выше информацию, следует начертить на нем таблицу с колонками:

● № п/п,
● задача,
● срочность,
● важность

● № п/п,
● задача,
● срочность,
● важность. Количество строк в зависимости от длины списка следует отрегулировать самостоятельно

Далее, на отдельном листочке нужно выписать все планы на завтра (когда будет приобретен навык работы с матрицей, это не понадобится). А после, исходя из их срочности – важности, необходимо распределить планы по соответствующим квадрантам

Количество строк в зависимости от длины списка следует отрегулировать самостоятельно.
Далее, на отдельном листочке нужно выписать все планы на завтра (когда будет приобретен навык работы с матрицей, это не понадобится)

А после, исходя из их срочности – важности, необходимо распределить планы по соответствующим квадрантам

Ввод данных и функционал

• В качестве элементов используются обыкновенные правильные дроби ( 1/2 , 29/7 , -1/125 ), десятичные дроби ( 12 , -0.01 , 3.14 ), а также числа в экспоненциальной форме ( 2.5e3 , 1e-2 ).
• Длина вводимых чисел ничем не ограничена, вводите хоть 1000 цифр, правда, возможно, придётся подождать, пока будут идти вычисления!
• Используйте для работы одну или две матрицы (чтобы выполнять операции с двумя матрицами, передвиньте переключатель второй матрицы).
• Вставляйте результат в A или B с помощью кнопок «Вставить в A» и «Вставить в B».
• Перетаскивайте (drag-and-drop) матрицы из результата в A или B.
• Используйте стрелки ( ← , ↑ , → , ↓ ) для перемещения по элементам

4.5 Печать графиков

Пункт Print в меню
File и команда print
печатают графику MatLab. Меню Print
вызывает диалоговое окно, которое
позволяет выбирать общие стандартные
варианты печати. Команда print
обеспечивает большую гибкость при
выводе выходных данных и позволяет
контролировать печать из М-файлов.
Результат может быть послан прямо на
принтер, выбранный по умолчанию, или
сохранен в заданном файле.

5. Примеры программ 

В этом разделе приведены
наиболее употребительные алгоритмы,
используемые при анализе многомерных
данных. Рассмотрены как простейшие
методы преобразования данных так и
алгоритмы для анализа данных — PCA, PLS.

NumPy массивы в Python

NumPy — это расширение для научных вычислений, которое поддерживает мощный объект N-мерного массива. Прежде чем использовать NumPy, необходимо установить его. Для получения дополнительной информации,

• Ознакомьтесь: Как установить NumPy Python?
• Если вы работаете в Windows, скачайте и установите дистрибутив anaconda Python. Он поставляется вместе с NumPy и другими расширениями.

После установки NumPy можно импортировать и использовать его.

NumPy предоставляет собой многомерный массив чисел (который на самом деле является объектом). Давайте рассмотрим приведенный ниже пример:

import numpy as np
a = np.array()
print(a)               # Вывод: 
print(type(a))         # Вывод: <class 'numpy.ndarray'>

Как видите, класс массива NumPy называется ndarray.

Основное назначение матрицы

Для того чтобы изготовить заготовку необходимой формы, используется матрица, которую можно сделать из:

Чтобы сделать железную деталь, матрицу необходимо изготовить из специализированной прочной стали, которая имеет высокую износоустойчивость. Подобная конструкция должна быть оборудована отполированными стенками и не иметь крышки.

Специалисты выделяют матрицы следующих видов:

Наиболее сложные конструктивные решения используются довольно редко, поэтому их производят по индивидуальному заказу. Примером простых матриц стоит считать формы для производства различных блоков и небольших кирпичей.

Объединяем трансформации : матрица ModelViewProjection

… Просто стандартные матричные преобразования, которые вы уже полюбили!

Совмещаем все вместе

Первый шаг — создание нашей MVP матрицы. Это должно быть сделано для каждой модели, которую вы отображаете.

Второй шаг — передать это в GLSL:

Третий шаг — используем полученные данные в GLSL, чтобы трансформировать наши вершины.

Готово! Теперь у нас есть такой же треугольник как и в Уроке 2, все так же находящийся в начале координат (0, 0, 0), но теперь мы его видим в перспективе из точки (4, 3, 3).

В Уроке 6 вы научитесь изменять эти значения динамически, используя клавиатуру и мышь, чтобы создать камеру, которую вы привыкли видеть в играх. Но для начала мы узнаем как придать нашем моделям цвета (Урок 4) и текстуры (Урок 5).

Задания

Попробуйте поменять значения glm::perspective
Вместо использования перспективной проекции попробуйте использовать ортогональную (glm:ortho)
Измените ModelMatrix для перемещения, поворота и масштабирования треугольника
Используйте предыдущее задание, но с разным порядком операций

Обратите внимание на результат.. Замечания

Замечания

1. И к счастью для нас, матрица 4х4 может выполнить эту проекцию: На самом деле, это не правильно. Перспективное преобразование не является аффинным и как таковое не может быть полностью представлено матрицей. После умножения на ProjectionMatrix однородные координаты делятся на свой собственный компонент W. Этой W-компонентой оказывается -Z (потому что проекционная матрица создана таким образом). Таким образом, точки, находящиеся далеко от начала координат, делятся на большое Z; их координаты X и Y становятся меньше; точки становятся ближе друг к другу, объекты кажутся меньше; и это то, что дает перспективу. Это преобразование выполняется в аппаратном обеспечении и не отображается в шейдере. 

Как сделать матрицу 4х4 в ворде

Работая в текстовом редакторе Ворд с нестандартными видами математических уравнений и формул, зачастую невозможно найти решение для вставки какого-то элемента. Вот, например, сделать матрицу в Ворде можно, но и здесь есть ограничения. На первый взгляд, кажется, что функционал ограничен и многие не знают, каким образом делается матрица 5 на 5 или 4 на 4, ведь нет такой структуры в допустимых вариантах. Максимальное значение, которое можно вставить это 3 на 3 – ошибочное мнение, которому подверглись многие пользователи Ворда. Давайте рассмотрим способ решения данной проблемы, и отныне для вас не будет границ в текстовом редакторе.

Где заказать?

Наша компания вот уже почти 15 лет работает на рынке резки и фрезеровки, мы располагаем современной технической базой, высокотехнологичными фрезерными ЧПУ-станками и опытным персоналом. Принимаем заказы на изготовление мастер-моделей для литья и болванов для матриц. Работаем преимущественно с деревом, МДФ, пенополистиролом и пластиком.

• создание 3д модели будущего изделия,
• вырезание на станке болван матрицы (или его деталей при необходимости сборки модели),
• доведение готового изделия до финишного результата (шлифовка, лакировка, покрытие специальными материалами – при необходимости и пожеланиях заказчика).

Сотрудничаем как с частными лицами, так и с корпоративными клиентами. К нам нередко обращаются для изготовления болванов для создания матриц, которые в дальнейшем будут использоваться при производстве катеров, запчастей автомобилей и другой техники.

Уточнить условия работы, сроки выполнения заказа, цены — можно связавшись с нами по телефону: +7 812 336-36-76.

Наше производство расположено в Санкт-Петербурге, но с работаем с клиентами из разных регионов, отправляя заказы посредством транспортных компаний.

редактор formula one

В разделе Образование на вопрос Как в Word в редакторе формул сделать вот это? заданный автором Просигнализировать лучший ответ это поставить большие скобки, потом внутри поставить матрицу и рядом с матрицей поставить черту вертикальную — там есть большая, где скобки, и добавить вектор-столбецЭто можно сделать точно! ! я так делала

22 ответа

Привет! Вот подборка тем с ответами на Ваш вопрос: Как в Word в редакторе формул сделать вот это?

Ответ от Дроздматрицу еще не пробовала рисовать, но не проще ли это как нибудь иначе все это оформить!!а вообще там должно быть такое, в специфических функциях

Ответ от LapochkaМожно!! Еще как можно! В редакторе формул есть. Не могу вставить фото, так бы показала. Придеться так объяснять…1. Открываешь редактор Формул2. Затем шаблоны скобок — выбираешь круглые скобки3. Затем шаблоны матриц — выбираешь 1Х4 в столбик (сверху третья в середине)4. Набираешь цифры которые после черты — Затем нажимаешь влево чтобы выйти из набора цифр5. затем опять шаблон скобок — выбираешь палочку прямую (снизу 2-й ряд, 2-я слева)6. Затем в этом квадратике — не уходи с него — выбираешь опять шаблон матриц7. Теперь уже выбираешь матрицу 4Х48. И набираешь цифрыВот и всеУспехов!!1

Ответ от НевропатологЭто невозможно, Word для этого не предназначен (для решения). Есть такой редактор формул MathType, с его помощью эта формула может попасть в Word. А найти эту надстройку не сложно,просто введите в Яндексе.

2 ответа

Привет! Вот еще темы с нужными ответами:

Матрица 4х4 в 2010 (2007) ворде . ru/ms-word/thread294301.html убрать пробел um. ru Историческая справка. Понятие Матрица было введено в работах У. Гамильтона и А. Кэли в середине 19 века. Основы теории созданы К. Вейерштрассом и Ф. Фробениусом (2-я половина 19 века и начало 20 века) . И. А. Лаппо-Данилевский разработал теорию аналитических функций от многих матричных аргументов и применил эту теорию к исследованию систем дифференциальных уравнений с аналитическими коэффициентами. Матричные обозначения получили распространение в современной математике и её приложениях. Исчисление М. развивается в направлении построения эффективных алгоритмов для численного решения основных задач.

Нажмите на кнопку Пуск и откройте Блокнот, введя блокнот в поле поиска. Если у вас Windows XP, нажмите Пуск, Выполнить и введите «notepad».

Умножение матриц

Матрицы умножаются по принципу строка на столбец. Мы умножаем первую строку первой матрицы, на первый столбец второй матрицы, складываем результаты и получаем первый элемент новой матрицы. По аналогичной схеме вычисляем все остальные элементы. Звучит запутанно, поэтому идём по шагам: 

1. У нас есть две матрицы A и B. Их нужно перемножить, чтобы получить новую матрицу C. 
2. Размер матрицы A два на два: есть две строки и два столбца. Первая строка состоит из элементов А₁₁ и А₁₂; вторая — А₂₁ и А₂₂. 
3. У матрицы B такая же размерность: есть две строки и два столбца. Первая строка состоит из элементов B₁₁ и B₁₂; вторая — B₂₁ и B₂₂. 
4. У нас две одинаковые по размеру матрицы с двумя строками и столбцами. Это значит, что и матрица C будет размером два на два. Первая строка будет состоять из элементов C₁₁ и C₁₂; вторая — C₂₁ и C₂₂. 
5. Считаем элемент C₁₁. Умножаем первый элемент первой строки матрицы А (А₁₁) на первый элемент первого столбика матрицы B (B₁₁). Это первая часть, после которой ставим знак плюс. Вторая часть: умножаем второй элемент первой строчки матрицы А (А₁₂) на второй элемент первого столбика матрицы B (B₂₁). Складываем обе части и получаем первый элемент первой строки матрицы С (C₁₁). 
6. Считаем элемент C₁₂. Умножаем первый элемент первой строки матрицы А (А₁₁) на первый элемент второго столбика матрицы B (B₁₂). Это первая часть. Вторая часть: умножаем второй элемент первой строчки матрицы А (А₁₂) на второй элемент второго столбика матрицы B (B₂₂). Складываем части и получаем второй элемент первой строки матрицы С (C₁₂). 
7. Считаем элемент C₂₁. Умножаем первый элемент второй строки матрицы А (А₂₁) на первый элемент первого столбика матрицы B (B₁₁). Это первая часть. Вторая часть: умножаем второй элемент второй строки матрицы А (А₂₂) на второй элемент первого столбика матрицы B (B₂₁). Складываем части и получаем первый элемент второй строки матрицы С (C₂₁). 
8. Считаем элемент C₂₂. Умножаем первый элемент второй строки матрицы А (А₂₁) на первый элемент второго столбика матрицы B (B₁₂). Это первая часть. Вторая часть: умножаем второй элемент второй строки матрицы А (А₂₂) на второй элемент второго столбика матрицы B (B₂₂). Складываем части и получаем второй элемент второй строки матрицы С (C₂₂). 

Если нам нужно найти матрицу в квадрате, то мы умножаем эту матрицу на саму себя. Если нужна матрица в кубе — умножаем её на саму себя три раза и так далее в зависимости от количества степеней. Если в одной из матриц все элементы нули, то она считается нулевой и после умножения на другую матрицу даёт нулевую матрицу — это как нуль умноженный на число всегда даёт нуль.

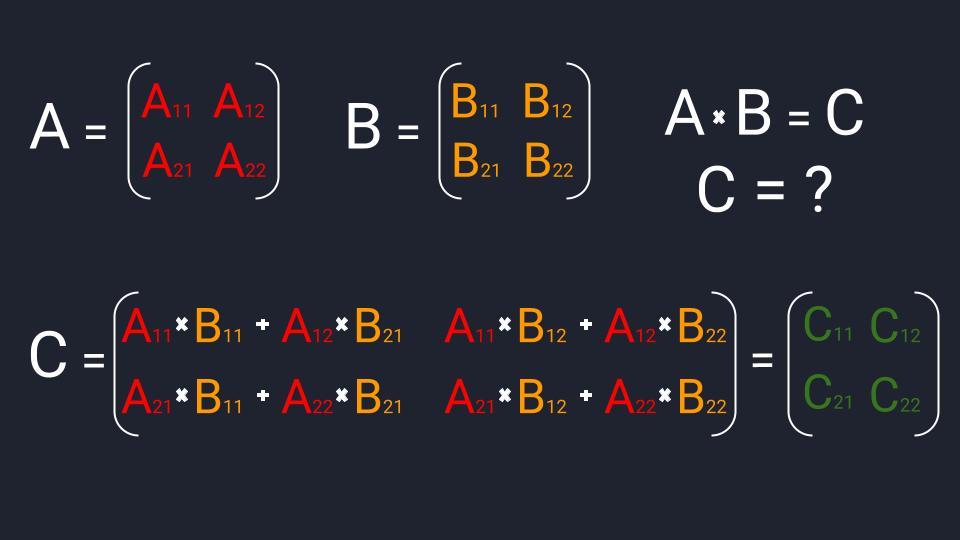Формула умножения матрицПример умножения квадратных матриц размерностью 2×2

Квадрант B: важно, но не срочно

Несмотря на то что это поле идёт по счету вторым, именно оно является самым важным. В рассматриваемый квадрат приоритетов Эйзенхауэра вписываются задачи, выполнение которых направлено на достижение актуальных целей:

● самообразование;
● выполнение текущих проектов на работе;
● выполнение обязанностей по дому;
● профилактика заболеваний, укрепление иммунитета.

Пример: до конца месяца (на календаре 3 мая) нужно сдать клиенту landing page. К данной задаче нужно приступить незамедлительно? Нет

Выполнение этого дела для карьеры важно? Однозначно.

Дела из квадрата B следует планировать и выполнять в отведенное для них время. В противном случае они приобретут срочный характер (перейдут в сектор А таблицы Эйзенхауэра) и станут причиной возникновения стресса.
Помните: неспешная реализация повседневных планов позволяет справляться с поставленной задачей качественно. А это, в свою очередь, возможность выйти на новый уровень финансового благополучия.

Как сделать матрицу в блокноте

Популярный научно-фантастический боевик Матрица вышел на экран более 15 лет назад и за это время успел завоевать любовь миллионов зрителей, став по истине легендарным и культовым кино. Долгое время на экранах мониторов по всему миру стояли обои и скринсейверы в стиле фильма — длинные завораживающие столбцы зеленых символов. Специально для фанатов кинокартины я расскажу о простом и несложном способе как можно создать матрицу в блокноте не используя при этом никаких подручных инструментов кроме имеющейся в операционной системе Windows 10 и командной строки. Поехали!

Создаём на рабочем столе текстовый файл. Например, matrix.txt. Открываем его в блокноте. Теперь надо скопировать туда следующие строчки:

Задаём заголовок окошка:

Задаём цвет символов:

Очищаем экран командной строки:

Создаём замкнутый цикл:

:prodolgit set stroka= for /l %%i in (0,1,78) do ( set /a vremenno=!random!%%2 set stroka=!stroka!!vremenno! ) set /a generate=!random!% if %generate%==0 (color 0A) else (color 02)

Выводим матрицу на экран:

echo %stroka% goto prodolgit

Сохраняемся и закрываем блокнот. Теперь надо переименовать файл, сменить ему расширение с *.txt на *.bat. После этого дважды кликаем по нему и получаем результат как на картинке выше. Как Вы видите этот способ как создать матрицу в блокноте очень простой и быстрый. Сделать может даже школьник!

Матрица на экране вашего компьютера.

Утилита Notepad считается простейшим текстовым редактором, годящимся не столько для редактирования быстро набранного текста, сколько простейшим представителем кодовых просмотрщиков. В связи с этим и можно использовать его возможности для проделывания простейших трюков, не требующих специальных навыков програмирования. На страницах блога Компьютер76 я покажу один из них.

Все смотрели фантастический фильм “Матрица”. В нескольких его кадрах появлялся ниспадающий код зелёного цвета из цифр и латинских букв на чёрном фоне по типу подбора программой уникального кода. Эта матрица на мониторе и стала своеобразным символом или визитной карточкой голливудской трилогии. Сделаем также с нашим компьютером. Ничего загружать из сети не нужно. Код матрицы будет транслироваться в консоли команд. Для компьютера матрица на экране монитора совершенно безвредна, единственный её минус – от ряби потихоньку начинаешь уставать. Но порой этот трюк придаёт помещению, в котором стоит компьютер, воспроизводящий бегающий код, некий потайной образ.

Откроем Notepad (он же Блокнот). Вставим туда вот этот текст (просто скопируйте его):

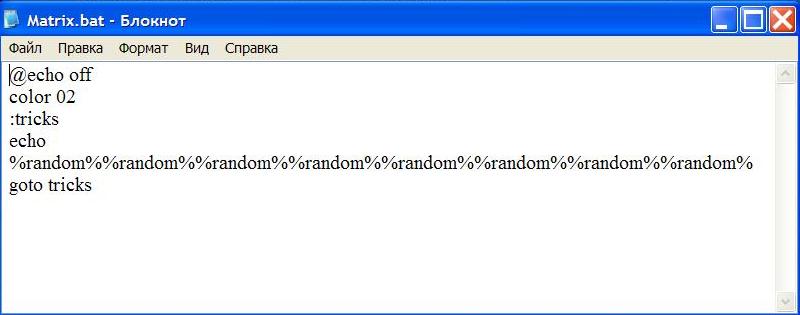
@echo off color 02 :tricks echo %random%%random%%random%%random%%random%%random%%random%%random% goto tricks

И закройте его, предварительно назвав новый документ… да как хотите, но обязательно присвоив расширение .bat. (У меня название Matrix). Должно получиться следующее:

Вот что мы увидим после двойного щелчка по файлу:

Для придания мистичности происходящего у вас на экране, можно развернуть окно консоли во весь экран, придав манер заставки или процесса взлома государственного учреждения (никак не меньше!), пока вы занимаетесь своими делами. Развернуть окно можно нажатием клавиш ALT + Enter. Вернуть к предыдущему размеру можно повторным нажатием этой же комбинации.

Найдены дубликаты

Вставить в блокнот

с расширением .bat

как скорость уменьшить?

Мы тож так в школе развлекались. Только вывод был не фиксированной длины, а непрерывный.

Матрица в Ворде

Работая в текстовом редакторе Ворд с нестандартными видами математических уравнений и формул, зачастую невозможно найти решение для вставки какого-то элемента. Вот, например, сделать матрицу в Ворде можно, но и здесь есть ограничения. На первый взгляд, кажется, что функционал ограничен и многие не знают, каким образом делается матрица 5 на 5 или 4 на 4, ведь нет такой структуры в допустимых вариантах. Максимальное значение, которое можно вставить это 3 на 3 – ошибочное мнение, которому подверглись многие пользователи Ворда. Давайте рассмотрим способ решения данной проблемы, и отныне для вас не будет границ в текстовом редакторе.

Как сделать матрицу для ковки

Однако, как можно изготовить матрицы для ковки своими руками, что для этого нужно и какими материалами воспользоваться?

Материал

Материал матрицы должен обладать высокими качествами, ведь готовый штамп будет постоянно соприкасаться с разогретыми заготовками, да и, к тому же, постоянно испытывать ударные, сжимающие нагрузки.

Для изготовления такого шаблона можно взять сталь с полуоси автомобиля, как показано на представленном видео:

Также можно сделать матрицу на поверхности бойка одного из рабочих молотов.

Или подойдет любой другой кусок стали с отличными свойствами противостоять деформации и сильному разогреву.

Что понадобиться

Есть виды штампов, которые изготавливают на фрезерном станке. Например, как на этом видео:

В предыдущем видео отлично показано, как сделать простейший тип матрицы — гусиную лапку, используя только болгарку, напильник и сварочный аппарат.

Процесс изготовления

• Для изготовления простого штампа гусиной лапки подготавливают заготовку. Ее поверхность выравнивают.
• На рабочей стороне нужно сделать разметку в виде расходящихся линий. Изначально отбивают центральную ось, а уже потом от нее два-три ответвления.
• Использую болгарку и отрезной круг, по линиям делают прорезы, углубляя их по краям.
• Работая угловой шлифовальной машиной, нужно сформировать по прорезям треугольные выступы.
• После чего весь рельеф дорабатывают напильником.
• Если изготавливается двухсторонняя обжимка, нужно с такого же куска материала сделать зеркальное отображение с выступами, точно совпадающими с впадинами на первой матрице.
• Обжимку соединяют в виде щипцов.
• Ударную сторону можно дополнительно усилить наваренным сверху бойком.
• Для удобного использования двухсторонней обжимки можно дополнительно изготовить ограничитель из трубы или другого подобного материала.
• Дополнительно сталь нужно закалить, чтобы повысить ее прочностные свойства.

А что Вы можете добавить к материалу этой статьи? Поделитесь своим опытом изготовления матриц для ковки металла, а также техниками их использования в кузнечных работах. Присоединяйтесь к обсуждениям в блоке комментариев к этой статье.

Источник

Болван матрица:

Чтобы изготовить любую матрицу — необходим болван для нее. Это прототип будущего изделия, в точности повторяющий его форму. При этом качество болвана должно быть очень высокое. Погрешности в размерах, форме, а также неровности и шероховатости поверхности — недопустимы.

Болван-матрица изготавливается либо из того же материала, что и конечное изделие, но чаще всего создается из любого чернового материала. Например, для изготовления матричных болванов нередко используют:

После финишной обработки болваны для матрицы обязательно шпатлюются, красятся и покрываются специальными лаками. Это необходимо для создания идеально гладкой непористой поверхности, что обеспечит глянцевую поверхность изделия и исключит возникновение эффекта «закипания».

Для создания сложных болванов используются фрезерные станки с ЧПУ (числовым программным управлением), которые позволяют создавать точные копии с минимальной погрешностью по размерам, при этом работают с различными материалами.

5.4 PLS1

Самым популярным способом для
многомерной калибровки является метод
проекции на латентные структуры (PLS). В
этом методе проводится одновременная
декомпозиция матрицы предикторов X и
матрицы откликов Y: 

X=TPt+E           
Y=UQt+F               
T=XW(PtW)–1

Проекция строится согласованно – так,
чтобы максимизировать корреляцию
между соответствующими векторами X-счетов
t_a и Y-счетов u_a.
Если блок данных Y включает
несколько откликов (т.е. K>1), можно
построить две проекции исходных данных
– PLS1 и PLS2. В первом случае для каждого из
откликов y_k строится свое
проекционное подпространство. При этом
и счета T (U) и нагрузки P (W, Q)
, зависят от того, какой отклик
используется. Этот подход называется PLS1.
Для метода PLS2 строится только одно
проекционное пространство, которое
является общим для всех откликов.

Детальное
описание метода PLS приведено в   Для построения PLS1 счетов и
нагрузок, используется рекуррентный
алгоритм. Сначала исходные матрицы X
и Y центрируют 

и они
превращаются в матрицу E и
вектор f, a=0. Далее к ним
применяет следующий алгоритм

После вычисления очередной (a-ой)
компоненты, полагаем t_a=t
и p_a=p. Для получения
следующей компоненты надо вычислить
остатки E_a+1 = E_a
– t pt и применить к ним тот
же алгоритм, заменив индекс a на a+1.

Приведем код этого алгоритма,
взятый из

О вычислении PLS1 с помощью
надстройки Chemometrics Add In рассказано в пособии